──人間なんてちっぽけな存在、人間同士が醜く争うなんて馬鹿馬鹿しいと思わないかな?──
※ブログ記事の内容に対して、及びリンク連絡以外のコメントはお控え下さい。関係無い内容のコメントに関しては此方から削除させて頂きます。
此処に来て一旦数ⅠAの問題に戻りますよー、何しろこっちの方が今回は難しかったので。
まずは第1問〔1〕の「数と式、方程式」。
基本の問題からまずはスタートの二日目の朝ですね。
まずは頭をこの問題からほぐしていきましょう。
まずはαを有理化していきます。手順を省かずに書くと下のようになるので確認しておいて下さい。
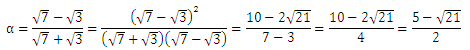
続いて
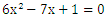
の計算をしていきます。
因数分解、すぐに出来たでしょうか?
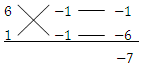
たすき掛けですね、6 = 6 × 1 、 1 = (-1) × (-1)と分解して考えます。
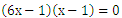
と因数分解できるので、答えは
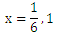
となります。
中学生の時や高一の時に習ったと思いますが、幾ら慣れていてもウッカリミスは必ずあります。
しっかり確認しながら進みましょう。
続いては下の4つの数を比べる作業。
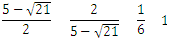
まずは有理化されていない2番目の数を有理化します。
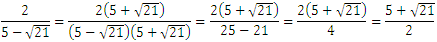
今回は小さいものを選べということなので、
1と、それより大きくなる 2/5-√21 (5+√21/2)は除外します。
残りの二つの決着ですが、まずは通分で
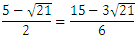
として、分子同士を比べます。
15-3√21と1は意外と近い値なのでパッと見判断しにくいですが、
こういう大小関係は引き算を使いましょう。
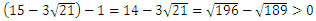
引き算した値が正となれば、大きいのは引かれる側の数。
つまり今回は15-3√21の方が大きいということになります。
以上から、最小の数は1/6ということになります。
続いて〔2〕の「集合と論理」。
条件は以下の4つ。
p : nは5で割ると1余る数である
q : nは10で割ると1余る数である
r : nは奇数である
s : nは2より大きい素数である
ちょっと日本語の解釈に困る(2より大きいって2を含めないんだろうけど)のもありますが。
(※あ、余談ですが、数学の問題を言葉のあやで間違ったことは何度もあります)
取りあえず、まずは具体的にしてみましょう。
p : 6 , 11 , 16 , 21 , ...
q : 11 , 21 , 31 , 41 , ...
r : 1 , 3 , 5 , 7 , 9 , 11 , ...
s : 3 , 5 , 7 , 11 , 13 , ...
論理で追うタイプの方はゴメンなさい、僕は基本、具体的に考えるタチなので…!
最初に
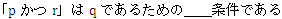
から解きましょう。
「pかつr」ということは、5で割ると1余るもののうちの奇数ということになります。
なので
p∩r : 11, 21 , 31 , 41 , ...
となります。
これは見れば分かりますが、qと全く同じ。
なので言うまでもなく 必要十分条件で結びましょう。
次に
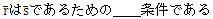
です。
 は奇数でない=偶数であるので
は奇数でない=偶数であるので
 : 2 , 4 , 6 , 8 , ...
: 2 , 4 , 6 , 8 , ...
となります。
そして
 は素数でない、なので
は素数でない、なので
 : 1 , 2 , 4 , 6 , 8 , 9 , ...
: 1 , 2 , 4 , 6 , 8 , 9 , ...
となります。
偶数である=素数でない なので、 →
→ は成り立ちます。
は成り立ちます。
しかし ←
← は成り立ちません。(反例:1 , 9などがある)
は成り立ちません。(反例:1 , 9などがある)
よって (十分条件)→(必要条件) なので、答えは十分条件です。
最後に
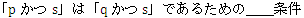
です。
「pかつs」は素数であり5で割ると1余る数なので
p∩s : 11 , 31 , 41 , 61 , ...
となります。
「qかつs」は
q∩s : 11 , 31 , 41 , 61, ...
となり、二つの条件が完全に一致するので必要十分条件となります。
(※自信がなければ10個ぐらいまで上げてみて下さい、納得出来ればで良いです)
最後に1問だけ残っていますね、少々珍しいド・モルガンの法則におけるベン図の使用です。
(※ベン図って何だったっけとかいう心配は要りません、見れば分かりますし、名前を覚えるべき用語って訳でもないので)
条件 p,r,s を満たす自然数全体の集合を、それぞれP,R,Sとした時に、
それらがどう重なり合っているか、という問題です。
P と R が一部重なり合っているのはすぐに分かると思います。
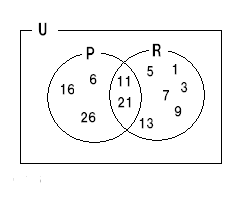
問題はSの領域です。
s : 3 , 5 , 7, 11 , 13 , ... ですので見た通り、R単独の領域にも、P∩Rの領域にも入ります。
条件sは素数であるので偶数は含まれないのでP単独の領域(6 ,16,26,...)には入りません。
なので答えは下図のようになります。
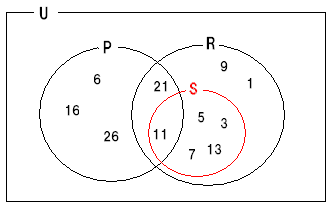
以上で数ⅠAの第1問の解説を終わります!
まずは第1問〔1〕の「数と式、方程式」。
基本の問題からまずはスタートの二日目の朝ですね。
まずは頭をこの問題からほぐしていきましょう。
まずはαを有理化していきます。手順を省かずに書くと下のようになるので確認しておいて下さい。
続いて
の計算をしていきます。
因数分解、すぐに出来たでしょうか?
たすき掛けですね、6 = 6 × 1 、 1 = (-1) × (-1)と分解して考えます。
と因数分解できるので、答えは
となります。
中学生の時や高一の時に習ったと思いますが、幾ら慣れていてもウッカリミスは必ずあります。
しっかり確認しながら進みましょう。
続いては下の4つの数を比べる作業。
まずは有理化されていない2番目の数を有理化します。
今回は小さいものを選べということなので、
1と、それより大きくなる 2/5-√21 (5+√21/2)は除外します。
残りの二つの決着ですが、まずは通分で
として、分子同士を比べます。
15-3√21と1は意外と近い値なのでパッと見判断しにくいですが、
こういう大小関係は引き算を使いましょう。
引き算した値が正となれば、大きいのは引かれる側の数。
つまり今回は15-3√21の方が大きいということになります。
以上から、最小の数は1/6ということになります。
続いて〔2〕の「集合と論理」。
条件は以下の4つ。
p : nは5で割ると1余る数である
q : nは10で割ると1余る数である
r : nは奇数である
s : nは2より大きい素数である
ちょっと日本語の解釈に困る(2より大きいって2を含めないんだろうけど)のもありますが。
(※あ、余談ですが、数学の問題を言葉のあやで間違ったことは何度もあります)
取りあえず、まずは具体的にしてみましょう。
p : 6 , 11 , 16 , 21 , ...
q : 11 , 21 , 31 , 41 , ...
r : 1 , 3 , 5 , 7 , 9 , 11 , ...
s : 3 , 5 , 7 , 11 , 13 , ...
論理で追うタイプの方はゴメンなさい、僕は基本、具体的に考えるタチなので…!
最初に
から解きましょう。
「pかつr」ということは、5で割ると1余るもののうちの奇数ということになります。
なので
p∩r : 11, 21 , 31 , 41 , ...
となります。
これは見れば分かりますが、qと全く同じ。
なので言うまでもなく 必要十分条件で結びましょう。
次に
です。
となります。
そして
となります。
偶数である=素数でない なので、
しかし
よって (十分条件)→(必要条件) なので、答えは十分条件です。
最後に
です。
「pかつs」は素数であり5で割ると1余る数なので
p∩s : 11 , 31 , 41 , 61 , ...
となります。
「qかつs」は
q∩s : 11 , 31 , 41 , 61, ...
となり、二つの条件が完全に一致するので必要十分条件となります。
(※自信がなければ10個ぐらいまで上げてみて下さい、納得出来ればで良いです)
最後に1問だけ残っていますね、少々珍しいド・モルガンの法則におけるベン図の使用です。
(※ベン図って何だったっけとかいう心配は要りません、見れば分かりますし、名前を覚えるべき用語って訳でもないので)
条件 p,r,s を満たす自然数全体の集合を、それぞれP,R,Sとした時に、
それらがどう重なり合っているか、という問題です。
P と R が一部重なり合っているのはすぐに分かると思います。
問題はSの領域です。
s : 3 , 5 , 7, 11 , 13 , ... ですので見た通り、R単独の領域にも、P∩Rの領域にも入ります。
条件sは素数であるので偶数は含まれないのでP単独の領域(6 ,16,26,...)には入りません。
なので答えは下図のようになります。
以上で数ⅠAの第1問の解説を終わります!
PR
この記事にコメントする
思い返せば2年くらい数学に触れてないという(ぇ
数1Aはちゃんと全部授業受けたはずなのに全然覚えてなくてorzしてましたサンライトです。
やっぱ使ってないと忘れるんですよねー…;
新聞には解説も何もないから教科書を引っ張ってくるしかないわけで。
段ボールの奥底にあったやつを見つけたはいいけど、はてどのページを見ればいいんだか?なレベルだったところにガーリィ先輩の解説!
助かりましたー、特に「集合と論理」の方。
なるほど、こうやって順番に書いてもらうとちゃんとわかるな。
これベン図って言うんですね。名前は知らなかったけど、学校じゃ集合の問題を解くときは面倒でも全部図を書けって教わってました。
ではー。
やっぱ使ってないと忘れるんですよねー…;
新聞には解説も何もないから教科書を引っ張ってくるしかないわけで。
段ボールの奥底にあったやつを見つけたはいいけど、はてどのページを見ればいいんだか?なレベルだったところにガーリィ先輩の解説!
助かりましたー、特に「集合と論理」の方。
なるほど、こうやって順番に書いてもらうとちゃんとわかるな。
これベン図って言うんですね。名前は知らなかったけど、学校じゃ集合の問題を解くときは面倒でも全部図を書けって教わってました。
ではー。
カレンダー
| 11 | 2025/12 | 01 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
フリーエリア
最新記事
最新TB
プロフィール
HN:
餅 雅李音(ガーリィ)
年齢:
36
HP:
性別:
男性
誕生日:
1989/06/07
職業:
大学院生
趣味:
ポケモン、恐竜、将棋、麻雀、 絵描き、小説書き (※創作全般に興味あり)
自己紹介:
ひたすら Going my way な道産子で関東圏の古生物専攻大学院生。
日本で数少ない地学系統に入る為に1年を平気で棒に振るようなお馬鹿さん。
将来の夢は古生物学者兼小説家。
平凡な人生を嫌う、My pace な駄犬。最近ドラゴン。
日本で数少ない地学系統に入る為に1年を平気で棒に振るようなお馬鹿さん。
将来の夢は古生物学者兼小説家。
平凡な人生を嫌う、My pace な駄犬。最近ドラゴン。
ブログ内検索
最古記事
P R
カウンター
