──人間なんてちっぽけな存在、人間同士が醜く争うなんて馬鹿馬鹿しいと思わないかな?──
※ブログ記事の内容に対して、及びリンク連絡以外のコメントはお控え下さい。関係無い内容のコメントに関しては此方から削除させて頂きます。
誰に謝るという訳でもなくて。
もしかしたら自分に謝っているのかもしれないし。
僕は今、色々と満たされていると思うんだ。
だけど、同時に満たされないことも沢山ある。
「もっとこれをやりたい」「もっとこうしたい」
そういう未来志向で、未然形なモノも沢山あるんだけど。
百歩譲ってそれは願望のままで終わるかもしれないと考えてみる。
実際そういう願望が最終的には出来ない事でも、それはそれで構わないと思うよ。
だけどそれ以上に、今までやって来た事が出来なくなっている。
そういう辛さが今の僕に纏わりついているんだ。
全てその時その時で満たされれば良い、それ以上は贅沢だ、そう考えれば楽になるのかもしれないけれど。
だけどそういう、今までやって来た事って、僕一人で作り上げたモノだけじゃないから。
僕一人がそう納得しても、誰かの心に穴を開けたままにするのはとても哀しいんだ。
欲張りだったのかもしれない、だけど、皆と一緒に何かをするってのは、本当に楽しいと思う。
ただ、行動範囲を広げ過ぎたんだ。
それが今の結果。
そして一度つまづくと、気不味い想いばかりが重なって、いつしか元に戻れなくなっている。
元々僕は、自分から行動はしないんだ。
しているようでしていない。
不思議なんだけど、先陣を切って行動する癖に、誰かに後押しされない限りは始めようとしないんだ、僕。
学級委員とか、そういう仕事は今でもやっているんだけどね。
でもトップには立たずにその後ろからトップを動かして、トップを気取る輩なんだ。
影の支配者、と言った方が良いのかもしれない。
ズルい輩だって事は百も承知しているから。
つまり簡単に言えば、僕はチキンだって話。
どんなに良いネタがあっても、一度切れちゃうとどうして良いのか分からなくなっちゃうんだ。
キッカケが必然であれ、偶然であれ、ね。
色々な事に当てはまり過ぎて困っちゃうけども。
正直、僕は今、何をしたら良いのか分からないんだ。
昔の引っ込み思案の僕に戻りつつあるのが分かるんだ。
誰かの声が聞けないと、どうしても寂しくて、淋しくて。
でもいざ聞こうとすると、その声が余りにも多過ぎて、自分の処理能力がパンクしているのも本当の話。
やっぱり。
潜った方が良いのかな、僕は。
ちょっと話はかわって。
僕の心は今、至って平和で平穏だと思う。
議論や闘争に熱くなる性格は持っているけれど、それとは別次元の気持ち、というか何というか。
ブログのサブタイトルにもあるように、妙に何処か達観した感覚を持っているのが僕。
ニンゲン同士の争いなんて、地球全体から見れば、宇宙全体から見れば、余りにちっぽけだから。
そんなちっぽけな行動が沢山集まって、今の世界が生まれているのも事実。
そしてそのちっぽけな行動を、僕自身も起こしている事も事実。
無常感に近いけど、ちょっと違う。
そんなちっぽけ行動が、愛おしくて仕方が無いから。
「どうせ何やったって生きて死ぬんだ」なんてどうにもならない気持ちを持ったってしょうがないもの。
「この命を輝かせたいんだ」って思う事の方が余程重要だもの。
自分がちっぽけだって分かった時、命を輝かせる方法も心構えも見えてくる筈なんだ。
些細な事ばかりだよ、そういう方法や心構えって。
人に優しくするってのも一つ。
人を認めるってのも一つ。
人を愛するってのも一つ。
命を愛おしいと思うことも一つ。
世界が素晴らしいって思うことも一つ。
生きていることに感謝するのも一つ。
勿論、宗教観とかそういうのは抜きにして、ね。
自分の素直な心を剥き出しにすると、自分自身、段々と心が満たされていくのが分かるんだ。
たいそうなことじゃなくたって良いんだ、元気に「おはよう!」と挨拶をするだけでも違ってくるんだし。
結局、寂しがり屋なんだけどね。
いつも誰かに、そして人の温かさに満たされていたい。
でもその気持ちが自分を優しくする原動力になるんだったら、それはそれでちょっぴり嬉しいかな。
アニメ、レジェンズのOP曲、「風のレジェンズ」。
そして、挿入歌、「空色の指先」。
あの二つの歌詞の気持ちそのものなんだな、と今更ながら気付いて。
前者の途中で出てくる、
「何よりも大好きな 素直な笑顔眺めて」ってところ。
誰かの幸せで、自分も幸せになれるんだ。
後者は丸々全部だけど、一部抜粋して。
「ふるえるほど嬉しい朝 涙が光って ほほえんでいるみたい」
「青い空が眩しすぎて 思わず瞼を ぎゅっとつぶっていたよ」
そんな些細な日々の出来事でも、見方をかえればこんなにも素晴らしかったんだ、そう思える瞬間。
心が荒んでしまっている人たちに、届けてあげたいんだ。
生きるってこんなに素晴らしいことなんだって。
精一杯生きることが、こんなにも素晴らしいことなんだって。
人は一人では生きていけない、その意味を自分の心で受け止められた瞬間。
世界はガラリと表情を変えるから不思議。
寂しがり屋だからこそ、満たされたい。
そして満たしてあげたい。
ただそれだけの気持ちなんだ。
それ以上でも、それ以下でもないよ。
おやすみなさい。
もしかしたら自分に謝っているのかもしれないし。
僕は今、色々と満たされていると思うんだ。
だけど、同時に満たされないことも沢山ある。
「もっとこれをやりたい」「もっとこうしたい」
そういう未来志向で、未然形なモノも沢山あるんだけど。
百歩譲ってそれは願望のままで終わるかもしれないと考えてみる。
実際そういう願望が最終的には出来ない事でも、それはそれで構わないと思うよ。
だけどそれ以上に、今までやって来た事が出来なくなっている。
そういう辛さが今の僕に纏わりついているんだ。
全てその時その時で満たされれば良い、それ以上は贅沢だ、そう考えれば楽になるのかもしれないけれど。
だけどそういう、今までやって来た事って、僕一人で作り上げたモノだけじゃないから。
僕一人がそう納得しても、誰かの心に穴を開けたままにするのはとても哀しいんだ。
欲張りだったのかもしれない、だけど、皆と一緒に何かをするってのは、本当に楽しいと思う。
ただ、行動範囲を広げ過ぎたんだ。
それが今の結果。
そして一度つまづくと、気不味い想いばかりが重なって、いつしか元に戻れなくなっている。
元々僕は、自分から行動はしないんだ。
しているようでしていない。
不思議なんだけど、先陣を切って行動する癖に、誰かに後押しされない限りは始めようとしないんだ、僕。
学級委員とか、そういう仕事は今でもやっているんだけどね。
でもトップには立たずにその後ろからトップを動かして、トップを気取る輩なんだ。
影の支配者、と言った方が良いのかもしれない。
ズルい輩だって事は百も承知しているから。
つまり簡単に言えば、僕はチキンだって話。
どんなに良いネタがあっても、一度切れちゃうとどうして良いのか分からなくなっちゃうんだ。
キッカケが必然であれ、偶然であれ、ね。
色々な事に当てはまり過ぎて困っちゃうけども。
正直、僕は今、何をしたら良いのか分からないんだ。
昔の引っ込み思案の僕に戻りつつあるのが分かるんだ。
誰かの声が聞けないと、どうしても寂しくて、淋しくて。
でもいざ聞こうとすると、その声が余りにも多過ぎて、自分の処理能力がパンクしているのも本当の話。
やっぱり。
潜った方が良いのかな、僕は。
ちょっと話はかわって。
僕の心は今、至って平和で平穏だと思う。
議論や闘争に熱くなる性格は持っているけれど、それとは別次元の気持ち、というか何というか。
ブログのサブタイトルにもあるように、妙に何処か達観した感覚を持っているのが僕。
ニンゲン同士の争いなんて、地球全体から見れば、宇宙全体から見れば、余りにちっぽけだから。
そんなちっぽけな行動が沢山集まって、今の世界が生まれているのも事実。
そしてそのちっぽけな行動を、僕自身も起こしている事も事実。
無常感に近いけど、ちょっと違う。
そんなちっぽけ行動が、愛おしくて仕方が無いから。
「どうせ何やったって生きて死ぬんだ」なんてどうにもならない気持ちを持ったってしょうがないもの。
「この命を輝かせたいんだ」って思う事の方が余程重要だもの。
自分がちっぽけだって分かった時、命を輝かせる方法も心構えも見えてくる筈なんだ。
些細な事ばかりだよ、そういう方法や心構えって。
人に優しくするってのも一つ。
人を認めるってのも一つ。
人を愛するってのも一つ。
命を愛おしいと思うことも一つ。
世界が素晴らしいって思うことも一つ。
生きていることに感謝するのも一つ。
勿論、宗教観とかそういうのは抜きにして、ね。
自分の素直な心を剥き出しにすると、自分自身、段々と心が満たされていくのが分かるんだ。
たいそうなことじゃなくたって良いんだ、元気に「おはよう!」と挨拶をするだけでも違ってくるんだし。
結局、寂しがり屋なんだけどね。
いつも誰かに、そして人の温かさに満たされていたい。
でもその気持ちが自分を優しくする原動力になるんだったら、それはそれでちょっぴり嬉しいかな。
アニメ、レジェンズのOP曲、「風のレジェンズ」。
そして、挿入歌、「空色の指先」。
あの二つの歌詞の気持ちそのものなんだな、と今更ながら気付いて。
前者の途中で出てくる、
「何よりも大好きな 素直な笑顔眺めて」ってところ。
誰かの幸せで、自分も幸せになれるんだ。
後者は丸々全部だけど、一部抜粋して。
「ふるえるほど嬉しい朝 涙が光って ほほえんでいるみたい」
「青い空が眩しすぎて 思わず瞼を ぎゅっとつぶっていたよ」
そんな些細な日々の出来事でも、見方をかえればこんなにも素晴らしかったんだ、そう思える瞬間。
心が荒んでしまっている人たちに、届けてあげたいんだ。
生きるってこんなに素晴らしいことなんだって。
精一杯生きることが、こんなにも素晴らしいことなんだって。
人は一人では生きていけない、その意味を自分の心で受け止められた瞬間。
世界はガラリと表情を変えるから不思議。
寂しがり屋だからこそ、満たされたい。
そして満たしてあげたい。
ただそれだけの気持ちなんだ。
それ以上でも、それ以下でもないよ。
おやすみなさい。
PR
おはようございます、ガーリィです。
最近ベッドで寝るのを止めて床寝し始めたら目覚めが快適になりましたー。
こんなに朝に強くなったのは久しぶりです、えぇ。
最近何時に寝ても8時半以降でないと起きられないのが続いていたので安心しましたー。
そんな訳で朝からレトルトのカレーをうまうま出来る訳です、うまうま。
はてさて、此処で報告があります。
以前から呟いていたネット将棋の大会ですが、予選が昨日で終わりましたー。
昨晩は対局が全く無かった(消化可能試合は全て消化していた)んですが、暫定トップのまま無事通過しましたー。
リーグ予選は試合消化が一番優先されるので結構必死でした。
参加登録したけど一戦も消化出来なかった方々もいらっしゃるんで、全試合消化はほぼ不可能なんですよねぇ。
強いけど消化出来ずに終わってしまった方もいらっしゃいます。
結局はモチベーションを如何に継続するかがカギなんだと思います。
最後の方はギリギリだった(1,2点勝負だった)んで、ちょっと自信になりました。
そんな訳で本戦に進むんですが、今度は何級リーグになるのやら。
最高レーティングを更新していないんで余り変わらないと思いますが──
上の級や段の方々はもっとハイレベルな対局をしていると思うと、まだまだだなぁと思ってしまいます。
初段以上のリーグで同じような報告が出来たら嬉しいんですけどねぇ。
そんな訳で、2週間後からまたまったりと始まりますが、頑張りたいと思います!
そろそろ他の事を書きたいなぁと思ったら、その2週間後ぐらいにポケモンの茨城予選も始まるんですよね!
準備に忙しい時期ですけど春休みはまだ来ない……!
あぅわぅー。
最近ベッドで寝るのを止めて床寝し始めたら目覚めが快適になりましたー。
こんなに朝に強くなったのは久しぶりです、えぇ。
最近何時に寝ても8時半以降でないと起きられないのが続いていたので安心しましたー。
そんな訳で朝からレトルトのカレーをうまうま出来る訳です、うまうま。
はてさて、此処で報告があります。
以前から呟いていたネット将棋の大会ですが、予選が昨日で終わりましたー。
昨晩は対局が全く無かった(消化可能試合は全て消化していた)んですが、暫定トップのまま無事通過しましたー。
リーグ予選は試合消化が一番優先されるので結構必死でした。
参加登録したけど一戦も消化出来なかった方々もいらっしゃるんで、全試合消化はほぼ不可能なんですよねぇ。
強いけど消化出来ずに終わってしまった方もいらっしゃいます。
結局はモチベーションを如何に継続するかがカギなんだと思います。
最後の方はギリギリだった(1,2点勝負だった)んで、ちょっと自信になりました。
そんな訳で本戦に進むんですが、今度は何級リーグになるのやら。
最高レーティングを更新していないんで余り変わらないと思いますが──
上の級や段の方々はもっとハイレベルな対局をしていると思うと、まだまだだなぁと思ってしまいます。
初段以上のリーグで同じような報告が出来たら嬉しいんですけどねぇ。
そんな訳で、2週間後からまたまったりと始まりますが、頑張りたいと思います!
そろそろ他の事を書きたいなぁと思ったら、その2週間後ぐらいにポケモンの茨城予選も始まるんですよね!
準備に忙しい時期ですけど春休みはまだ来ない……!
あぅわぅー。
何だか随分経っちゃいましたけど、お久しぶりです、ガーリィです。
センター解説の方は前回の記事で終わりにしたいと思います。
てか2月になっちゃいましたしねー。
また気が向いたら何か書くかもしれませんが、それは後程──。
まぁ、期間が空いたから色々と報告しなきゃいけないんですが。
まずはネット将棋の大会の方。
予選5級60人リーグに参戦中ですが、残り3日間を残して勝ち点でトップに立ちました。
最も有名なネット将棋のサイトなんで知っている方も居るかもしれませんが。
第一pixivとほぼ同じアカウント(スペースがあるか無いか)なんで探せばすぐ見つかりますけどね!
pixivと将棋クラブ24のアカウントを両方持っていて活動している人ってどの位居るんでしょう、摩訶不思議。
あ、サイト名出ちゃいました。
予選だけでなく本戦もこの調子で行ければ良いなぁと願うばかりです。
リアルの方の生活はというと。
ほとんどの大学生の皆さんは、もう休みに入ったか、テスト期間かのどちらかなんでしょうけど。
ウチは3月頭に最終授業があるんで2月は休みではないです。
なのでオフしようぜ! とか、遊びに行こうぜ! と誘われても反応出来ないと思います、ゴメンなさい…!
第一今バイトが出来ない代わりに節約で貯金していこうと思っている最中なのでー。
勿論夏の福井上陸の為ですよ! えぇ!
一応就活に近い意義もあるので気が抜けません…!
(その道に就いた方に直接お話を聞けるチャンスですからねー)
とまぁ、色々ありますけど。
近づいているのはテストとポケモンワールドチャンピオンシップスの茨城予選。
後一匹が決定していません、ぷぎゃー。
何はともあれ頑張ります! ふぁいおー!
センター解説の方は前回の記事で終わりにしたいと思います。
てか2月になっちゃいましたしねー。
また気が向いたら何か書くかもしれませんが、それは後程──。
まぁ、期間が空いたから色々と報告しなきゃいけないんですが。
まずはネット将棋の大会の方。
予選5級60人リーグに参戦中ですが、残り3日間を残して勝ち点でトップに立ちました。
最も有名なネット将棋のサイトなんで知っている方も居るかもしれませんが。
第一pixivとほぼ同じアカウント(スペースがあるか無いか)なんで探せばすぐ見つかりますけどね!
pixivと将棋クラブ24のアカウントを両方持っていて活動している人ってどの位居るんでしょう、摩訶不思議。
あ、サイト名出ちゃいました。
予選だけでなく本戦もこの調子で行ければ良いなぁと願うばかりです。
リアルの方の生活はというと。
ほとんどの大学生の皆さんは、もう休みに入ったか、テスト期間かのどちらかなんでしょうけど。
ウチは3月頭に最終授業があるんで2月は休みではないです。
なのでオフしようぜ! とか、遊びに行こうぜ! と誘われても反応出来ないと思います、ゴメンなさい…!
第一今バイトが出来ない代わりに節約で貯金していこうと思っている最中なのでー。
勿論夏の福井上陸の為ですよ! えぇ!
一応就活に近い意義もあるので気が抜けません…!
(その道に就いた方に直接お話を聞けるチャンスですからねー)
とまぁ、色々ありますけど。
近づいているのはテストとポケモンワールドチャンピオンシップスの茨城予選。
後一匹が決定していません、ぷぎゃー。
何はともあれ頑張ります! ふぁいおー!
遅れましたが数ⅠAの解答解説の続きです!
と、此処で二つお詫びしなければいけないことがあります。
一つ目は、数式が余りに多くて、
Wordからプリントスクリーンをして画像フォルダにして貼り付けるという手法を取っていると
余りに時間がかかる分野に突入しています。
なので此処から先はWordに書いた解答解説をそのまま貼り付けます。
PDFファイルにしたんですがアップロードの仕方が面倒でした……!
(※PCからの閲覧推奨は変わりません)
そしてもう一つ、既に各予備校さんの方で解答解説が出てしまっていることです。
それじゃ意味が無いじゃないか! と思ってしまいそうなんですが、此処は生き残りをかけて。
「此処の解説もっと詳しくしてくれよ!」という部分が残りの分野にありましたら教えて下さると助かります!
分かっている前提で話を進められても分かんねぇよ、という声には出来る限り応えたいので!
宜しくお願いします……!
それでは数学IAの第3問「2次関数」、スタート!



何か疑問がありましたら気軽にどうぞー!
と、此処で二つお詫びしなければいけないことがあります。
一つ目は、数式が余りに多くて、
Wordからプリントスクリーンをして画像フォルダにして貼り付けるという手法を取っていると
余りに時間がかかる分野に突入しています。
なので此処から先はWordに書いた解答解説をそのまま貼り付けます。
PDFファイルにしたんですがアップロードの仕方が面倒でした……!
(※PCからの閲覧推奨は変わりません)
そしてもう一つ、既に各予備校さんの方で解答解説が出てしまっていることです。
それじゃ意味が無いじゃないか! と思ってしまいそうなんですが、此処は生き残りをかけて。
「此処の解説もっと詳しくしてくれよ!」という部分が残りの分野にありましたら教えて下さると助かります!
分かっている前提で話を進められても分かんねぇよ、という声には出来る限り応えたいので!
宜しくお願いします……!
それでは数学IAの第3問「2次関数」、スタート!
何か疑問がありましたら気軽にどうぞー!
此処に来て一旦数ⅠAの問題に戻りますよー、何しろこっちの方が今回は難しかったので。
まずは第1問〔1〕の「数と式、方程式」。
基本の問題からまずはスタートの二日目の朝ですね。
まずは頭をこの問題からほぐしていきましょう。
まずはαを有理化していきます。手順を省かずに書くと下のようになるので確認しておいて下さい。
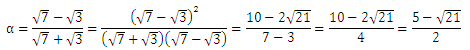
続いて
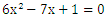
の計算をしていきます。
因数分解、すぐに出来たでしょうか?
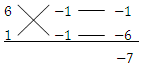
たすき掛けですね、6 = 6 × 1 、 1 = (-1) × (-1)と分解して考えます。
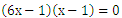
と因数分解できるので、答えは
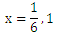
となります。
中学生の時や高一の時に習ったと思いますが、幾ら慣れていてもウッカリミスは必ずあります。
しっかり確認しながら進みましょう。
続いては下の4つの数を比べる作業。
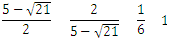
まずは有理化されていない2番目の数を有理化します。
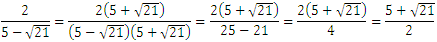
今回は小さいものを選べということなので、
1と、それより大きくなる 2/5-√21 (5+√21/2)は除外します。
残りの二つの決着ですが、まずは通分で
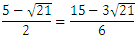
として、分子同士を比べます。
15-3√21と1は意外と近い値なのでパッと見判断しにくいですが、
こういう大小関係は引き算を使いましょう。
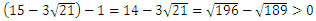
引き算した値が正となれば、大きいのは引かれる側の数。
つまり今回は15-3√21の方が大きいということになります。
以上から、最小の数は1/6ということになります。
続いて〔2〕の「集合と論理」。
条件は以下の4つ。
p : nは5で割ると1余る数である
q : nは10で割ると1余る数である
r : nは奇数である
s : nは2より大きい素数である
ちょっと日本語の解釈に困る(2より大きいって2を含めないんだろうけど)のもありますが。
(※あ、余談ですが、数学の問題を言葉のあやで間違ったことは何度もあります)
取りあえず、まずは具体的にしてみましょう。
p : 6 , 11 , 16 , 21 , ...
q : 11 , 21 , 31 , 41 , ...
r : 1 , 3 , 5 , 7 , 9 , 11 , ...
s : 3 , 5 , 7 , 11 , 13 , ...
論理で追うタイプの方はゴメンなさい、僕は基本、具体的に考えるタチなので…!
最初に
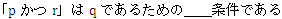
から解きましょう。
「pかつr」ということは、5で割ると1余るもののうちの奇数ということになります。
なので
p∩r : 11, 21 , 31 , 41 , ...
となります。
これは見れば分かりますが、qと全く同じ。
なので言うまでもなく 必要十分条件で結びましょう。
次に
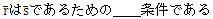
です。
 は奇数でない=偶数であるので
は奇数でない=偶数であるので
 : 2 , 4 , 6 , 8 , ...
: 2 , 4 , 6 , 8 , ...
となります。
そして
 は素数でない、なので
は素数でない、なので
 : 1 , 2 , 4 , 6 , 8 , 9 , ...
: 1 , 2 , 4 , 6 , 8 , 9 , ...
となります。
偶数である=素数でない なので、 →
→ は成り立ちます。
は成り立ちます。
しかし ←
← は成り立ちません。(反例:1 , 9などがある)
は成り立ちません。(反例:1 , 9などがある)
よって (十分条件)→(必要条件) なので、答えは十分条件です。
最後に
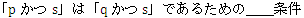
です。
「pかつs」は素数であり5で割ると1余る数なので
p∩s : 11 , 31 , 41 , 61 , ...
となります。
「qかつs」は
q∩s : 11 , 31 , 41 , 61, ...
となり、二つの条件が完全に一致するので必要十分条件となります。
(※自信がなければ10個ぐらいまで上げてみて下さい、納得出来ればで良いです)
最後に1問だけ残っていますね、少々珍しいド・モルガンの法則におけるベン図の使用です。
(※ベン図って何だったっけとかいう心配は要りません、見れば分かりますし、名前を覚えるべき用語って訳でもないので)
条件 p,r,s を満たす自然数全体の集合を、それぞれP,R,Sとした時に、
それらがどう重なり合っているか、という問題です。
P と R が一部重なり合っているのはすぐに分かると思います。
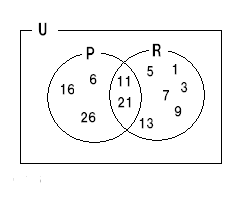
問題はSの領域です。
s : 3 , 5 , 7, 11 , 13 , ... ですので見た通り、R単独の領域にも、P∩Rの領域にも入ります。
条件sは素数であるので偶数は含まれないのでP単独の領域(6 ,16,26,...)には入りません。
なので答えは下図のようになります。
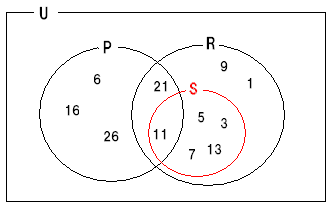
以上で数ⅠAの第1問の解説を終わります!
まずは第1問〔1〕の「数と式、方程式」。
基本の問題からまずはスタートの二日目の朝ですね。
まずは頭をこの問題からほぐしていきましょう。
まずはαを有理化していきます。手順を省かずに書くと下のようになるので確認しておいて下さい。
続いて
の計算をしていきます。
因数分解、すぐに出来たでしょうか?
たすき掛けですね、6 = 6 × 1 、 1 = (-1) × (-1)と分解して考えます。
と因数分解できるので、答えは
となります。
中学生の時や高一の時に習ったと思いますが、幾ら慣れていてもウッカリミスは必ずあります。
しっかり確認しながら進みましょう。
続いては下の4つの数を比べる作業。
まずは有理化されていない2番目の数を有理化します。
今回は小さいものを選べということなので、
1と、それより大きくなる 2/5-√21 (5+√21/2)は除外します。
残りの二つの決着ですが、まずは通分で
として、分子同士を比べます。
15-3√21と1は意外と近い値なのでパッと見判断しにくいですが、
こういう大小関係は引き算を使いましょう。
引き算した値が正となれば、大きいのは引かれる側の数。
つまり今回は15-3√21の方が大きいということになります。
以上から、最小の数は1/6ということになります。
続いて〔2〕の「集合と論理」。
条件は以下の4つ。
p : nは5で割ると1余る数である
q : nは10で割ると1余る数である
r : nは奇数である
s : nは2より大きい素数である
ちょっと日本語の解釈に困る(2より大きいって2を含めないんだろうけど)のもありますが。
(※あ、余談ですが、数学の問題を言葉のあやで間違ったことは何度もあります)
取りあえず、まずは具体的にしてみましょう。
p : 6 , 11 , 16 , 21 , ...
q : 11 , 21 , 31 , 41 , ...
r : 1 , 3 , 5 , 7 , 9 , 11 , ...
s : 3 , 5 , 7 , 11 , 13 , ...
論理で追うタイプの方はゴメンなさい、僕は基本、具体的に考えるタチなので…!
最初に
から解きましょう。
「pかつr」ということは、5で割ると1余るもののうちの奇数ということになります。
なので
p∩r : 11, 21 , 31 , 41 , ...
となります。
これは見れば分かりますが、qと全く同じ。
なので言うまでもなく 必要十分条件で結びましょう。
次に
です。
となります。
そして
となります。
偶数である=素数でない なので、
しかし
よって (十分条件)→(必要条件) なので、答えは十分条件です。
最後に
です。
「pかつs」は素数であり5で割ると1余る数なので
p∩s : 11 , 31 , 41 , 61 , ...
となります。
「qかつs」は
q∩s : 11 , 31 , 41 , 61, ...
となり、二つの条件が完全に一致するので必要十分条件となります。
(※自信がなければ10個ぐらいまで上げてみて下さい、納得出来ればで良いです)
最後に1問だけ残っていますね、少々珍しいド・モルガンの法則におけるベン図の使用です。
(※ベン図って何だったっけとかいう心配は要りません、見れば分かりますし、名前を覚えるべき用語って訳でもないので)
条件 p,r,s を満たす自然数全体の集合を、それぞれP,R,Sとした時に、
それらがどう重なり合っているか、という問題です。
P と R が一部重なり合っているのはすぐに分かると思います。
問題はSの領域です。
s : 3 , 5 , 7, 11 , 13 , ... ですので見た通り、R単独の領域にも、P∩Rの領域にも入ります。
条件sは素数であるので偶数は含まれないのでP単独の領域(6 ,16,26,...)には入りません。
なので答えは下図のようになります。
以上で数ⅠAの第1問の解説を終わります!
カレンダー
| 10 | 2025/11 | 12 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
フリーエリア
最新記事
最新TB
プロフィール
HN:
餅 雅李音(ガーリィ)
年齢:
36
HP:
性別:
男性
誕生日:
1989/06/07
職業:
大学院生
趣味:
ポケモン、恐竜、将棋、麻雀、 絵描き、小説書き (※創作全般に興味あり)
自己紹介:
ひたすら Going my way な道産子で関東圏の古生物専攻大学院生。
日本で数少ない地学系統に入る為に1年を平気で棒に振るようなお馬鹿さん。
将来の夢は古生物学者兼小説家。
平凡な人生を嫌う、My pace な駄犬。最近ドラゴン。
日本で数少ない地学系統に入る為に1年を平気で棒に振るようなお馬鹿さん。
将来の夢は古生物学者兼小説家。
平凡な人生を嫌う、My pace な駄犬。最近ドラゴン。
ブログ内検索
最古記事
P R
カウンター
