──人間なんてちっぽけな存在、人間同士が醜く争うなんて馬鹿馬鹿しいと思わないかな?──
※ブログ記事の内容に対して、及びリンク連絡以外のコメントはお控え下さい。関係無い内容のコメントに関しては此方から削除させて頂きます。
遅れましたが数ⅠAの解答解説の続きです!
と、此処で二つお詫びしなければいけないことがあります。
一つ目は、数式が余りに多くて、
Wordからプリントスクリーンをして画像フォルダにして貼り付けるという手法を取っていると
余りに時間がかかる分野に突入しています。
なので此処から先はWordに書いた解答解説をそのまま貼り付けます。
PDFファイルにしたんですがアップロードの仕方が面倒でした……!
(※PCからの閲覧推奨は変わりません)
そしてもう一つ、既に各予備校さんの方で解答解説が出てしまっていることです。
それじゃ意味が無いじゃないか! と思ってしまいそうなんですが、此処は生き残りをかけて。
「此処の解説もっと詳しくしてくれよ!」という部分が残りの分野にありましたら教えて下さると助かります!
分かっている前提で話を進められても分かんねぇよ、という声には出来る限り応えたいので!
宜しくお願いします……!
それでは数学IAの第3問「2次関数」、スタート!



何か疑問がありましたら気軽にどうぞー!
と、此処で二つお詫びしなければいけないことがあります。
一つ目は、数式が余りに多くて、
Wordからプリントスクリーンをして画像フォルダにして貼り付けるという手法を取っていると
余りに時間がかかる分野に突入しています。
なので此処から先はWordに書いた解答解説をそのまま貼り付けます。
PDFファイルにしたんですがアップロードの仕方が面倒でした……!
(※PCからの閲覧推奨は変わりません)
そしてもう一つ、既に各予備校さんの方で解答解説が出てしまっていることです。
それじゃ意味が無いじゃないか! と思ってしまいそうなんですが、此処は生き残りをかけて。
「此処の解説もっと詳しくしてくれよ!」という部分が残りの分野にありましたら教えて下さると助かります!
分かっている前提で話を進められても分かんねぇよ、という声には出来る限り応えたいので!
宜しくお願いします……!
それでは数学IAの第3問「2次関数」、スタート!
何か疑問がありましたら気軽にどうぞー!
PR
此処に来て一旦数ⅠAの問題に戻りますよー、何しろこっちの方が今回は難しかったので。
まずは第1問〔1〕の「数と式、方程式」。
基本の問題からまずはスタートの二日目の朝ですね。
まずは頭をこの問題からほぐしていきましょう。
まずはαを有理化していきます。手順を省かずに書くと下のようになるので確認しておいて下さい。
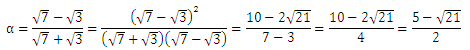
続いて
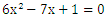
の計算をしていきます。
因数分解、すぐに出来たでしょうか?
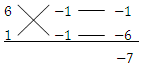
たすき掛けですね、6 = 6 × 1 、 1 = (-1) × (-1)と分解して考えます。
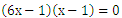
と因数分解できるので、答えは
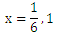
となります。
中学生の時や高一の時に習ったと思いますが、幾ら慣れていてもウッカリミスは必ずあります。
しっかり確認しながら進みましょう。
続いては下の4つの数を比べる作業。
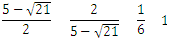
まずは有理化されていない2番目の数を有理化します。
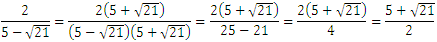
今回は小さいものを選べということなので、
1と、それより大きくなる 2/5-√21 (5+√21/2)は除外します。
残りの二つの決着ですが、まずは通分で
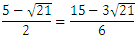
として、分子同士を比べます。
15-3√21と1は意外と近い値なのでパッと見判断しにくいですが、
こういう大小関係は引き算を使いましょう。
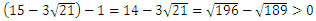
引き算した値が正となれば、大きいのは引かれる側の数。
つまり今回は15-3√21の方が大きいということになります。
以上から、最小の数は1/6ということになります。
続いて〔2〕の「集合と論理」。
条件は以下の4つ。
p : nは5で割ると1余る数である
q : nは10で割ると1余る数である
r : nは奇数である
s : nは2より大きい素数である
ちょっと日本語の解釈に困る(2より大きいって2を含めないんだろうけど)のもありますが。
(※あ、余談ですが、数学の問題を言葉のあやで間違ったことは何度もあります)
取りあえず、まずは具体的にしてみましょう。
p : 6 , 11 , 16 , 21 , ...
q : 11 , 21 , 31 , 41 , ...
r : 1 , 3 , 5 , 7 , 9 , 11 , ...
s : 3 , 5 , 7 , 11 , 13 , ...
論理で追うタイプの方はゴメンなさい、僕は基本、具体的に考えるタチなので…!
最初に
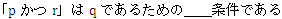
から解きましょう。
「pかつr」ということは、5で割ると1余るもののうちの奇数ということになります。
なので
p∩r : 11, 21 , 31 , 41 , ...
となります。
これは見れば分かりますが、qと全く同じ。
なので言うまでもなく 必要十分条件で結びましょう。
次に
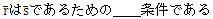
です。
 は奇数でない=偶数であるので
は奇数でない=偶数であるので
 : 2 , 4 , 6 , 8 , ...
: 2 , 4 , 6 , 8 , ...
となります。
そして
 は素数でない、なので
は素数でない、なので
 : 1 , 2 , 4 , 6 , 8 , 9 , ...
: 1 , 2 , 4 , 6 , 8 , 9 , ...
となります。
偶数である=素数でない なので、 →
→ は成り立ちます。
は成り立ちます。
しかし ←
← は成り立ちません。(反例:1 , 9などがある)
は成り立ちません。(反例:1 , 9などがある)
よって (十分条件)→(必要条件) なので、答えは十分条件です。
最後に
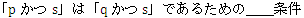
です。
「pかつs」は素数であり5で割ると1余る数なので
p∩s : 11 , 31 , 41 , 61 , ...
となります。
「qかつs」は
q∩s : 11 , 31 , 41 , 61, ...
となり、二つの条件が完全に一致するので必要十分条件となります。
(※自信がなければ10個ぐらいまで上げてみて下さい、納得出来ればで良いです)
最後に1問だけ残っていますね、少々珍しいド・モルガンの法則におけるベン図の使用です。
(※ベン図って何だったっけとかいう心配は要りません、見れば分かりますし、名前を覚えるべき用語って訳でもないので)
条件 p,r,s を満たす自然数全体の集合を、それぞれP,R,Sとした時に、
それらがどう重なり合っているか、という問題です。
P と R が一部重なり合っているのはすぐに分かると思います。
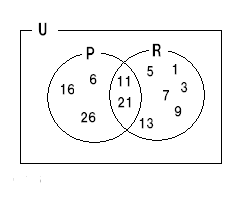
問題はSの領域です。
s : 3 , 5 , 7, 11 , 13 , ... ですので見た通り、R単独の領域にも、P∩Rの領域にも入ります。
条件sは素数であるので偶数は含まれないのでP単独の領域(6 ,16,26,...)には入りません。
なので答えは下図のようになります。
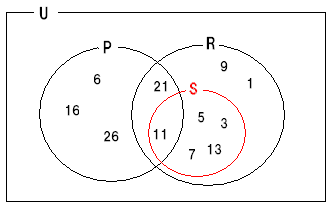
以上で数ⅠAの第1問の解説を終わります!
まずは第1問〔1〕の「数と式、方程式」。
基本の問題からまずはスタートの二日目の朝ですね。
まずは頭をこの問題からほぐしていきましょう。
まずはαを有理化していきます。手順を省かずに書くと下のようになるので確認しておいて下さい。
続いて
の計算をしていきます。
因数分解、すぐに出来たでしょうか?
たすき掛けですね、6 = 6 × 1 、 1 = (-1) × (-1)と分解して考えます。
と因数分解できるので、答えは
となります。
中学生の時や高一の時に習ったと思いますが、幾ら慣れていてもウッカリミスは必ずあります。
しっかり確認しながら進みましょう。
続いては下の4つの数を比べる作業。
まずは有理化されていない2番目の数を有理化します。
今回は小さいものを選べということなので、
1と、それより大きくなる 2/5-√21 (5+√21/2)は除外します。
残りの二つの決着ですが、まずは通分で
として、分子同士を比べます。
15-3√21と1は意外と近い値なのでパッと見判断しにくいですが、
こういう大小関係は引き算を使いましょう。
引き算した値が正となれば、大きいのは引かれる側の数。
つまり今回は15-3√21の方が大きいということになります。
以上から、最小の数は1/6ということになります。
続いて〔2〕の「集合と論理」。
条件は以下の4つ。
p : nは5で割ると1余る数である
q : nは10で割ると1余る数である
r : nは奇数である
s : nは2より大きい素数である
ちょっと日本語の解釈に困る(2より大きいって2を含めないんだろうけど)のもありますが。
(※あ、余談ですが、数学の問題を言葉のあやで間違ったことは何度もあります)
取りあえず、まずは具体的にしてみましょう。
p : 6 , 11 , 16 , 21 , ...
q : 11 , 21 , 31 , 41 , ...
r : 1 , 3 , 5 , 7 , 9 , 11 , ...
s : 3 , 5 , 7 , 11 , 13 , ...
論理で追うタイプの方はゴメンなさい、僕は基本、具体的に考えるタチなので…!
最初に
から解きましょう。
「pかつr」ということは、5で割ると1余るもののうちの奇数ということになります。
なので
p∩r : 11, 21 , 31 , 41 , ...
となります。
これは見れば分かりますが、qと全く同じ。
なので言うまでもなく 必要十分条件で結びましょう。
次に
です。
となります。
そして
となります。
偶数である=素数でない なので、
しかし
よって (十分条件)→(必要条件) なので、答えは十分条件です。
最後に
です。
「pかつs」は素数であり5で割ると1余る数なので
p∩s : 11 , 31 , 41 , 61 , ...
となります。
「qかつs」は
q∩s : 11 , 31 , 41 , 61, ...
となり、二つの条件が完全に一致するので必要十分条件となります。
(※自信がなければ10個ぐらいまで上げてみて下さい、納得出来ればで良いです)
最後に1問だけ残っていますね、少々珍しいド・モルガンの法則におけるベン図の使用です。
(※ベン図って何だったっけとかいう心配は要りません、見れば分かりますし、名前を覚えるべき用語って訳でもないので)
条件 p,r,s を満たす自然数全体の集合を、それぞれP,R,Sとした時に、
それらがどう重なり合っているか、という問題です。
P と R が一部重なり合っているのはすぐに分かると思います。
問題はSの領域です。
s : 3 , 5 , 7, 11 , 13 , ... ですので見た通り、R単独の領域にも、P∩Rの領域にも入ります。
条件sは素数であるので偶数は含まれないのでP単独の領域(6 ,16,26,...)には入りません。
なので答えは下図のようになります。
以上で数ⅠAの第1問の解説を終わります!
Part.3は「数ⅡB」の途中から!
あ、Part.1間違って消しちゃったみたいなんですが、直すのも今更なんでちゃんとした解説を改めて載せます。
(※携帯表示だと途中の式が出ないかもしれません、あらかじめご了承下さい)
第1問の〔2〕は「三角関数」。
二倍角の公式やら何やらのフル活用をしないといけない問題です。
最後がちょっと難しかったかもしれませんが全体的にスムーズな流れになっています。
0 < θ < π/2 の範囲での sin4θ = cosθ …① を解く問題。
勿論4倍角の公式(?)なんて使いませんから不安にならないように。
あ、Part.1間違って消しちゃったみたいなんですが、直すのも今更なんでちゃんとした解説を改めて載せます。
(※携帯表示だと途中の式が出ないかもしれません、あらかじめご了承下さい)
第1問の〔2〕は「三角関数」。
二倍角の公式やら何やらのフル活用をしないといけない問題です。
最後がちょっと難しかったかもしれませんが全体的にスムーズな流れになっています。
0 < θ < π/2 の範囲での sin4θ = cosθ …① を解く問題。
勿論4倍角の公式(?)なんて使いませんから不安にならないように。
取りあえずまずはcosをsinに直して両辺ともsinにしてしまいましょう。
0 < θ < π/2 (0°~90°)の範囲なのであの公式を使います。
最初の答えの式は θ ではなく x でしたけども。
なので最初の式①は sin4θ = sin(π/2 - θ) になります。
つまり 4θ と π/2 - θ が同じならOK、そう思ってイコールで結ぶだけだと失敗します。
三角関数はとられる範囲によっては同じ値が幾つも出てくる(例: sinπ/6 = sin5/6π = sin13/6π = ...)ので答えは一つとは限りません。
誘導にもある通り、0 < θ < π/2 の範囲で決まります。
-1<sin4θ<1 かつ 0<sin(π/2 - θ)<1 なので、この2つの値は2回一致することになります(下図参照)。
sin4θ は緑の値を2度とり、sin(π/2 - θ) は緑の値を1度だけとるので、組み合わせは2×1=2通り。
なので 4θ = π/2 - θ か 4θ = π - (π/2 - θ) のどちらかを満たせばOKです。
(この辺ピンと来なかったら取りあえず誘導に乗ってみましょう)
それぞれを解いてあげると θ = π/6 または θ = π/10 が出てきます。
続いて sinπ/10の値を求めに行きますが、ここでセンターならではの誘導がかかります。
最初の①の式に戻って──
と突き進みます(赤文字が x になったり θ になったりしたのはミスです)。
両辺に cosθ がありますが、cosθ は0 < θ < π/2 の範囲では cosθ >0 なので両辺割れます。
(0になる可能性がある時は割ってはいけません! 例えば 4×0 = 5×0 を両辺0で割ったりすると 4=5 となっておかしくなってしまいます)
cosθ で割ってから左辺に整理すると、 8sin3θ - 4sinθ + 1 = 0 ……② が出てきます。
後はこれを因数分解すれば良いんですが、ここで先程のもう一つの解である θ = π/6 が役に立ちます。
sinπ/6 = 1/2が①の式で既に成り立っているので、②の式の解の一つが sinθ = 1/2 (⇔ sinθ - 1/2 = 0 ⇔ 2sinθ - 1 = 0) になります。
つまり②を因数分解すると (2sinθ - 1) が因数として登場する、という訳です!
(※解が一つだけ分かっている時にこの考え方は有効です)
それを踏まえて②を因数分解しますと──
ここで、sinθ ≠ 1/2 であるので、
となります。
後はこれを解の公式で解けば θ = π/10 の時の答えが出てくる訳です。
答えは二つ出てきますが、sinπ/10 > 0 なので──
が答えになります。
解の公式は
がスタンダードですけど、bが2の倍数の時は──
の方が慣れると使い勝手が宜しいですよー。
とんでもなく長くなりましたが以上で第1問〔2〕の三角関数の解説を終わりますー!
今回のPart.2は「数ⅡB」からスタート!
(※携帯表示だと途中の式が出ないかもしれません、あらかじめご了承下さい)
第1問〔1〕は「対数関数」。
これも例年通りですね、慣れている人には解き易かったと思います。
ここは得点源! 是非満点で切り抜けて欲しいです。
解答の流れを以下に示します、毎回似たような流れなので何度も練習しましょうー。
まずはxy=128の両辺の対数をとれと言われているので素直にlog2をとります。
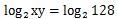
左辺はlogの中身が掛け算なので分解します。右辺は──
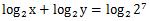
となるので右辺は
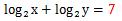
となります。最初の答えの7が出ます。
そして次にこの
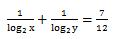
という式を解きます。両辺にlog2xとlog2yをかけて、
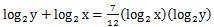
この左辺はさっき解いたので7。
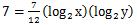
後は12/7を両辺にかければOKです。
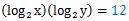
で、log2xとlog2yについて、和と積が出たので、次の式のtの解がこの2つの答えになります。
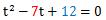
これはよく使われる和と積の問題ですので覚えておくと便利ですー。
で、これからt=3,4が出るので、
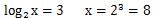
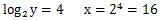
と答えがそれぞれ出ます。勿論この逆の答えもありですので答えは(x,y)=(8,16),(16,8)の2種類となります。
と、ここまで書いたところでタイムアップ!
第2問以降は後日順番に考察していきたいと思いますー。
今年受験生の皆さんも、来年以降受験の皆さんも、それぞれ頑張って下さいね!
(※携帯表示だと途中の式が出ないかもしれません、あらかじめご了承下さい)
第1問〔1〕は「対数関数」。
これも例年通りですね、慣れている人には解き易かったと思います。
ここは得点源! 是非満点で切り抜けて欲しいです。
解答の流れを以下に示します、毎回似たような流れなので何度も練習しましょうー。
まずはxy=128の両辺の対数をとれと言われているので素直にlog2をとります。
左辺はlogの中身が掛け算なので分解します。右辺は──
となるので右辺は
となります。最初の答えの7が出ます。
そして次にこの
という式を解きます。両辺にlog2xとlog2yをかけて、
この左辺はさっき解いたので7。
後は12/7を両辺にかければOKです。
で、log2xとlog2yについて、和と積が出たので、次の式のtの解がこの2つの答えになります。
これはよく使われる和と積の問題ですので覚えておくと便利ですー。
で、これからt=3,4が出るので、
と答えがそれぞれ出ます。勿論この逆の答えもありですので答えは(x,y)=(8,16),(16,8)の2種類となります。
と、ここまで書いたところでタイムアップ!
第2問以降は後日順番に考察していきたいと思いますー。
今年受験生の皆さんも、来年以降受験の皆さんも、それぞれ頑張って下さいね!
今日のクラスセミナーの時間に思わず怒ってしまいました。
というより、キレてしまったような気もします。
大学じゃそういう意味で怒ることが無いように、そう思っていたんですけども。
まぁ多分、お腹が減っているのに餅をせっせと焼かされて、ずっと食べられなかった所為もあるんでしょうね!
皆手伝えよ! 手伝わないなら焦げたとか文句言うなよ! そうでなくてもガスコンロ直火だから調節難しいのに!
きっとキッカケは些細な事だったんでしょうけど、相手が小馬鹿にしたような態度だから気持ちが悪いもんです。
ずっとヘラヘラ笑っている人が一番嫌いなもので。
取りあえず、落ち着こうか僕。
不要に当たってしまった相手には後で謝っておこうと思います、わぅーん。
反省。
でもやっぱり、自分の弱さを実感せざるを得ませんでした。
「他人は自分の思い通りにならない」
そう分かっている筈なのに、なかなか自分が言う事を聞かない瞬間って出てきてしまうんだな、と。
今回はその事に気づけただけでも良かったと思います。
自分がどんなに正しいと思ったって、相手にとってはそう出来ない事も沢山あります。
能力や気力、体力、そしてその時の状況によって。
幾ら正論でも「無理強い」になる事も多々あります。
例えばの話──
正月休みやお盆休みの最中にいつものようにメールして、返信が来ない事に腹を立てる、とか。
相手が必死こいて勉強している最中に遊びの催促をして、断られたら腹を立てる、とか。
明らかな「無理強い」になってしまう事は明白でしょう。
前者だったら幾ら自分が暇でも相手は忙しい事だって沢山ありますし。
それでも返信してくれる人は居ます、けどそれは自分に不満を持って欲しくないからしてくれているんです。
本来だったら迷惑行為にだってなりかねない事を。
後者も同様です。
自分が大学の推薦に受かったからって他の一般受験する人の邪魔をして良い訳がありませんし。
応援するか、見守るか、それしか出来ない筈です。
これらは、相手に対する配慮が欠けた瞬間に生まれる事を覚えておいて下さい。
因みに、これらの行為は──後から気付けば良いですが──僕は間違いなく首を振ります。
中身が幾ら正論であっても。
肝心の”心”が抜けている間は、正論も意味を成さない事は自分でもよく実感しています。
実際、今日もそうだったかもしれません。
もう一度、ゆっくり風呂にでも浸かって、いつものように集中して、頭の中を整理したいと思います。
集中力だけは半端ないって実感はありますし。
それこそ他の全てを忘れて──食べる事すら忘れて──数日間同じ事をやって退けた経験はあるので。
折角なのでその能力を生かしていきたいと思います。
追記
以前の友人からも年賀状が届きました、ありがとう、皆!
皆それぞれの道を歩んでいて何だか嬉しかったよー!
僕も頑張るから! 皆もふぁいおー!
ネット将棋の名人戦予選、今のところ6勝4敗です。
というより、キレてしまったような気もします。
大学じゃそういう意味で怒ることが無いように、そう思っていたんですけども。
まぁ多分、お腹が減っているのに餅をせっせと焼かされて、ずっと食べられなかった所為もあるんでしょうね!
皆手伝えよ! 手伝わないなら焦げたとか文句言うなよ! そうでなくてもガスコンロ直火だから調節難しいのに!
きっとキッカケは些細な事だったんでしょうけど、相手が小馬鹿にしたような態度だから気持ちが悪いもんです。
ずっとヘラヘラ笑っている人が一番嫌いなもので。
取りあえず、落ち着こうか僕。
不要に当たってしまった相手には後で謝っておこうと思います、わぅーん。
反省。
でもやっぱり、自分の弱さを実感せざるを得ませんでした。
「他人は自分の思い通りにならない」
そう分かっている筈なのに、なかなか自分が言う事を聞かない瞬間って出てきてしまうんだな、と。
今回はその事に気づけただけでも良かったと思います。
自分がどんなに正しいと思ったって、相手にとってはそう出来ない事も沢山あります。
能力や気力、体力、そしてその時の状況によって。
幾ら正論でも「無理強い」になる事も多々あります。
例えばの話──
正月休みやお盆休みの最中にいつものようにメールして、返信が来ない事に腹を立てる、とか。
相手が必死こいて勉強している最中に遊びの催促をして、断られたら腹を立てる、とか。
明らかな「無理強い」になってしまう事は明白でしょう。
前者だったら幾ら自分が暇でも相手は忙しい事だって沢山ありますし。
それでも返信してくれる人は居ます、けどそれは自分に不満を持って欲しくないからしてくれているんです。
本来だったら迷惑行為にだってなりかねない事を。
後者も同様です。
自分が大学の推薦に受かったからって他の一般受験する人の邪魔をして良い訳がありませんし。
応援するか、見守るか、それしか出来ない筈です。
これらは、相手に対する配慮が欠けた瞬間に生まれる事を覚えておいて下さい。
因みに、これらの行為は──後から気付けば良いですが──僕は間違いなく首を振ります。
中身が幾ら正論であっても。
肝心の”心”が抜けている間は、正論も意味を成さない事は自分でもよく実感しています。
実際、今日もそうだったかもしれません。
もう一度、ゆっくり風呂にでも浸かって、いつものように集中して、頭の中を整理したいと思います。
集中力だけは半端ないって実感はありますし。
それこそ他の全てを忘れて──食べる事すら忘れて──数日間同じ事をやって退けた経験はあるので。
折角なのでその能力を生かしていきたいと思います。
追記
以前の友人からも年賀状が届きました、ありがとう、皆!
皆それぞれの道を歩んでいて何だか嬉しかったよー!
僕も頑張るから! 皆もふぁいおー!
ネット将棋の名人戦予選、今のところ6勝4敗です。
カレンダー
| 10 | 2025/11 | 12 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
フリーエリア
最新記事
最新TB
プロフィール
HN:
餅 雅李音(ガーリィ)
年齢:
36
HP:
性別:
男性
誕生日:
1989/06/07
職業:
大学院生
趣味:
ポケモン、恐竜、将棋、麻雀、 絵描き、小説書き (※創作全般に興味あり)
自己紹介:
ひたすら Going my way な道産子で関東圏の古生物専攻大学院生。
日本で数少ない地学系統に入る為に1年を平気で棒に振るようなお馬鹿さん。
将来の夢は古生物学者兼小説家。
平凡な人生を嫌う、My pace な駄犬。最近ドラゴン。
日本で数少ない地学系統に入る為に1年を平気で棒に振るようなお馬鹿さん。
将来の夢は古生物学者兼小説家。
平凡な人生を嫌う、My pace な駄犬。最近ドラゴン。
ブログ内検索
最古記事
P R
カウンター
